In common usage, chaos means a state of utter confusion, but in regards to dynamical systems it usually refers to the behavior of simple systems that exhibit complex nonrepetitive motion. These are systems whose dynamics are known and can be accurately described by a small number of equations. Given these equations and the initial state of the system the future dynamics can be calculated using a computer. It seems surprising at first that simple systems can exhibit such complicated motion. The emergence of fast electronic computers starting in the 1960s provided an important tool that was needed to fully study them. As a result, chaos became the focus of a great deal of research. One of the main goals of this research has been to better understand how the dynamics can change from very simple periodic behavior to chaos. The Fleet Center has two exhibits that demonstrate chaotic behavior: one is a double pendulum and the other is a two dimensional pendulum that interacts with some permanent magnets mounted beneath.

In order to study a dynamical system, one needs to be able to specify precisely its state at any particular moment in time. For example, the state of the Fleet Center's double pendulum exhibit could be given by the angles of the two arms (relative to straight down) combined with the rates at which those two angles are changing in time, making 4 variables altogether. Using Newton's laws of motion, it is straightforward to write down the equations of motion for these 4 variables that would describe how the double pendulum would move over time from some given initial state. In addition, there is a small amount of dissipation caused by friction in the joints and also by air resistance to the motion of the arms that will cause the motion to slowly lose energy and decay in amplitude. This dissipation can be approximately modeled in the equations if desired.

The Chaotic pendulums at the Fleet Center are somewhat different from chaotic systems that are typically studied. Such typical systems usually have significant dissipation that takes energy out of the system, but unlike the Fleet pendulums, they also have some ongoing excitation or forcing mechanism by which energy enters the system. This long-term behavior will (typically) not decay to zero but rather will either approach a simple periodic oscillation or a complicated chaotic motion. The Fleet pendulums on the other hand, have very low dissipation of energy and, after being set in motion, no additional energy input. As their motion slowly decays, it will typically transition between more complex behavior (at higher amplitudes) to simple periodic behavior (at low amplitudes) and approach zero motion as time goes to infinity.

Chaotic systems have a sensitivity to initial conditions. This can be problematic if you are trying to model the behavior of a real physical system using its equations of motion. Even if the equations are known precisely, this sensitivity means that an extremely small disturbance or error in the initial state of the system will grow exponentially over time and will make long term prediction impossible. This is the case, for example, in trying to predict the weather far into the future. The term "butterfly effect" is often used in this regard; one is to imagine that a slight change such as the flapping of butterfly's wings would likely result in large scale weather changes a few weeks later such as the path of a tornado on the opposite side of the earth.

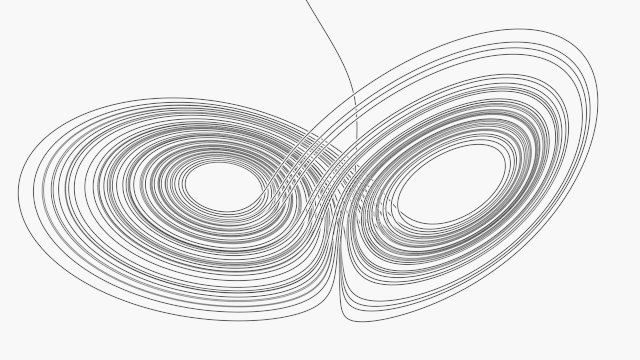
The variables that specify the state of a system, such as the 4 variables needed for the double pendulum, are often thought of as coordinates in an imaginary space known as phase space. Every point in this space is a distinct possible state of the system. As the system evolves in time it follows a path in the phase space but it does not wander randomly, rather it stays on a structure known as the attractor. Let's consider a simple case first: if the dynamics is not chaotic but rather a simple periodic motion, then the attractor will be a simple closed path in the phase space, similar to a car doing laps around a race track. It isn't necessarily a circular path, but it is a closed circuit. If you start the system anywhere on this attractor it will continue to move on the attractor. If you a start it slightly off of the attractor the motion will approach the attractor over time, similar to a car entering a racetrack tangentially and gradually merging into the flow. In the case of chaos, there is still an attractor, but it is no longer a closed path; it is something much more complex called a strange attractor. One way to visualize an attractor is to plot one variable against another one. For the double pendulum you could, for example, plot the angle of one arm of the pendulum vs the rate of change of that angle. This type of plot is known as a phase portrait. One of the first chaotic systems to be studied in detail using computers was the Lorenz system which was developed in 1963 by Edward Lorenz, a mathematician and meteorologist. It is a very simple set of equations intended to crudely model atmospheric convection. Lorenz was surprised to discover that his equations produced such complex dynamics. The figure at the top of this page shows a phase portrait for the Lorenz system when it is chaotic. The path starts off of the attractor at the top of the image, but quickly merges with the strange attractor. It is a fractal, which means that if you zoom in on part of the attractor you will continue to see finer and finer details.

The structure of a strange attractor can often be seen more clearly by looking at a cross section. Imagine that we can cut through the attractor and look at the exposed surface. This is called a Poincaré section. The figure below shows the Poincaré section for another well known system, the Duffing equation, for a particular set of parameters (sometimes called the Ueda attractor or the Japanese attractor). Note that the image is made up of thousands of dots where the path passes through the surface. As before, if you magnify any part of the strange attractor you just see more structure on finer and finer scales.