The Sikus exhibit consists of a series of tubes that resonate or vibrate at different frequencies. If place your ear at the end of one of the tubes you can hear a slightly noisy tone at the frequency of that tube. The longer tubes have lower frequencies than the shorter tubes. If you change the length of a tube by sliding the end up or down you can change the pitch of a given tube. The tubes are excited by background noise in the room which is normally a mixture of all frequencies.

The Whack-A-Phone exhibit is similarly a series of tubes of different lengths. An important difference though, is that in this case the exhibit is designed to be a musical instrument, with the tube lengths adjusted to match the 8 notes of one octave (white notes only). A tube is excited in this case by whacking the tube end with a rubber paddle. This creates a pressure transient in the tube, exciting the fundamental and harmonic vibrations of that tube.

Actually it's the confined air, not the tube itself, that vibrates. This resonance is related to the speed of sound in the air. The fact that sound takes some time to get from one place to another is commonly observed in echos from buildings or cliffs and also in the time delay between seeing a lightning flash and hearing the thunder. At 70 degrees Farenheit sound travels at about 1128 feet per second (or 343 meters per second). Sound is a pressure wave that travels through the air. The figure below shows a traveling sound wave moving left to right. The vertical axis shows the small oscillating fluctuations in the air pressure as the wave moves past. At sea level the average pressure is about 14.7 pounds per square inch or PSI. As a sound wave moves past you, the pressure fluctuates slightly, repeatedly moving up and down relative to this average value. The rate of up and down fluctuation is the frequency of the sound wave. If the sound corresponds to middle C on a piano keyboard, then this fluctuation frequency is about 262 cycles per second. Your eardrum is made to vibrate at this rate by the fluctuating pressure and your brain interprets this vibration as a tone.

The sound of a single pure tone has a particular wavelength. This is similar to water waves in the ocean, where the crests of the waves have a certain distance between them. The pressure peaks in a sound wave have a similar spacing. To find the wavelength, you just divide the speed of sound by the frequency, so for middle C that's 1128/262 or a little over 4 feet.

When you have a tube, like in the Sikus exhibit, a sound wave can be trapped inside the tube. However, because the tube has ends, the sound wave has to fit in the tube. It turns out that for a tube with both ends open, like the Sikus and most flutes, approximately one half cycle will fit in the tube. The reason is that the relative pressure must go approximately to zero at the open ends. There are also higher frequencies that will fit in the tube but we will only consider in detail the lowest frequency, which is called the fundamental. (The higher frequencies are multiples fundamental frequency and are called harmonics.) Half a cycle is close to 2 feet for middle C, and this is in fact about the length of a flute that has a low note of middle C.

Imagine we could start the oscillation with the air slightly accumulated towards the center of the tube so that the pressure is slightly higher there than at the ends of the tube. This pressure causes the air to accelerate outwards in both directions away from the center, simultaneously going towards both of the end holes. The air at the exact center remains motionless. This process takes some time because the mass of the air gives it inertia. As the air flows outwards, its pressure decreases and its velocity increases. After a short while, the relative pressure reaches zero, and the speed is at a maximum at the two exit holes where it is moving in opposite directions. When passing the exit holes, the outgoing air is suddenly free to escape in all directions, and this has the effect of keeping the relative pressure there close to zero throughout the cycle of vibration. Because of momentum, the air continues to flow outwards, away from the center, causing the pressure in the center of the tube to go below the average pressure. This causes the air to begin to slow down. Eventually, the air speed reaches zero and reverses, starting to go back into the tube. The pressure in the center begins increasing and eventually ends up above the average pressure, close to the pressure at which we started. This cycle repeats and is fairly efficient, losing only a little bit of energy each time, mostly escaping as sound waves emitted from the ends of the tube. The air pressure inside the tube oscillates in a standing wave as shown in the figure below. 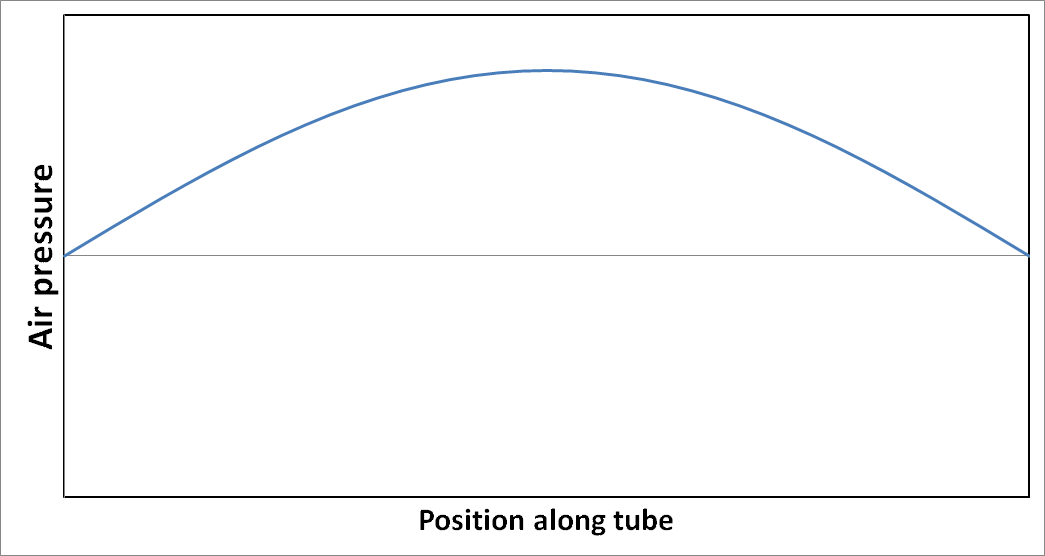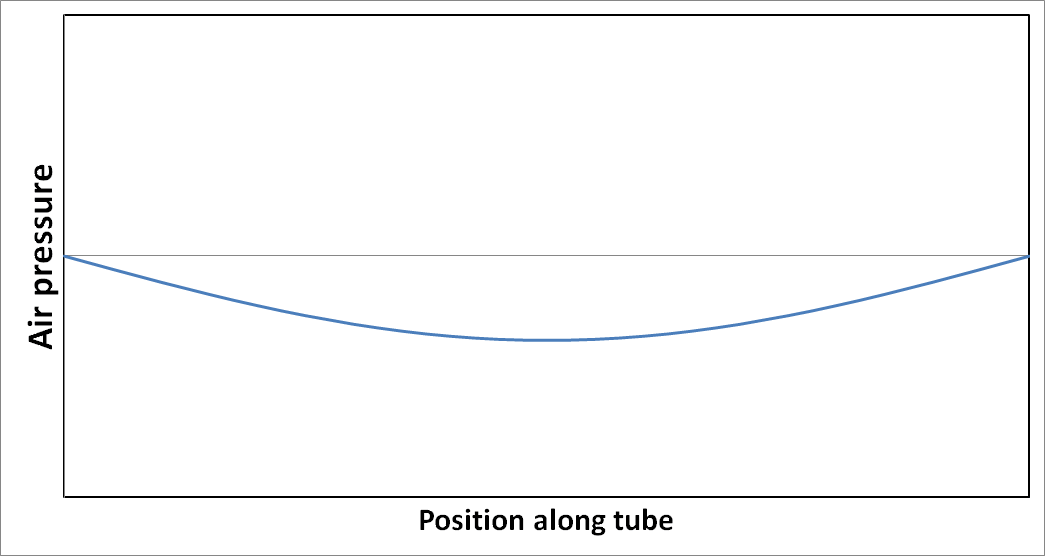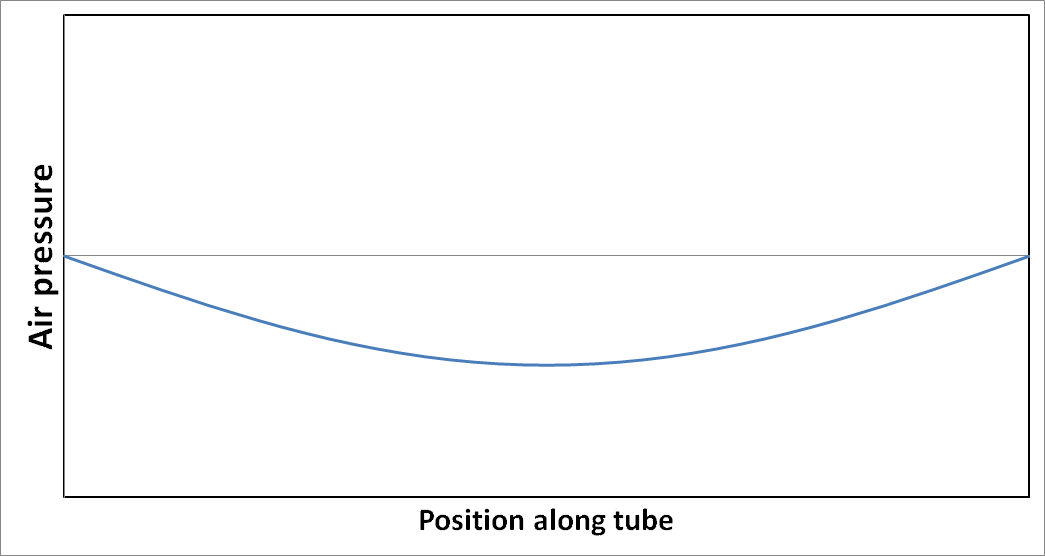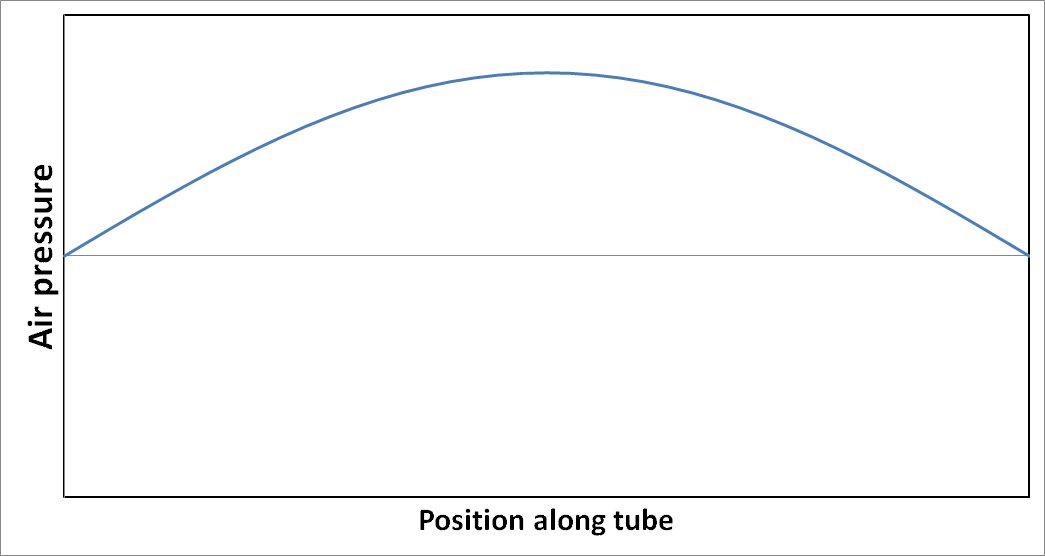Note that the pressure remains close to zero near the ends. This wave will slowly decay to zero over many cycles, unless continuously excited by room noise or by someone striking the end of the tube. Note also that for low level excitation, only a small percentage of the air actually leaves and reenters the ends of the tube.

For a pure tone, a sound wave takes the form of a mathematical function known as a sine wave. It can be obtained as a solution of the equations of motion which can be found in most elementary physics textbooks. We will not show this derivation here. Stringed instruments also exhibit standing waves, though in that case the wave appears as the side to side motion of the string.